The MSCI World equity market entered a trendless phase for a few months, with high but progressively amortized oscillations.
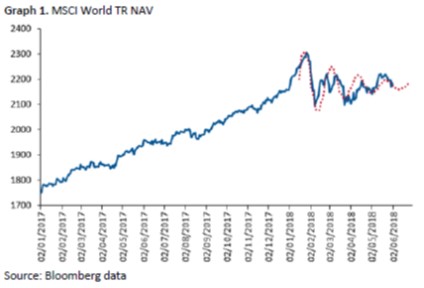
This type of phenomenon is not explained by portfolio theories and is very similar to the physics of waves, from optics to quantum physics.
So, let’s first compare the financial understanding of a volatility spike with that of quantum physics, and then run an experiment on the S&P500.
Which one is right?
In statistical finance, the future of an asset market is represented by the distribution of returns. The distribution is like a quantum wave: a representation of probable states that will materialize over time.
Statistical finance believes financial markets have no memory. In other words, what is happening in the market today has no influence on what may happen tomorrow, even on a probabilistic basis. The distribution of future returns is not affected by current market observations. Hence, the measure of an investment portfolio value-at-risk should barely be affected by last month’s equity price behavior.
The following illustration represents a wave of returns along the axis of time. A realized return on a specific day is equivalent to a measure of the wave function. The measure collapses all possible states into a single observable return at time T. Then the wave starts again, unaffected.
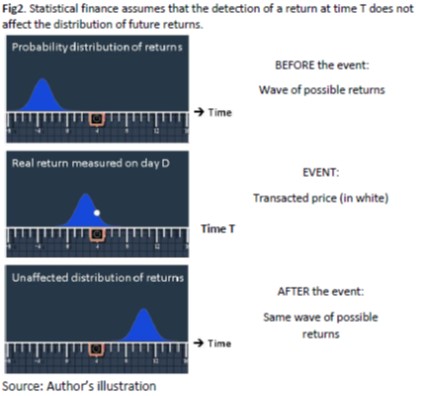
Quantum physics states exactly the opposite. Waves are constantly reshaped by measurements. The physical world has a memory of past interactions, and such a memory drives the future probable states of the world. Let’s now simulate the evolution of a quantum wave, thanks to the Schrödinger equation, before and after interacting with a measurement instrument.
The act of measuring the wave, like in finance, collapses the wave. The difference is that the detector is a physical object, not a point. It has a certain expansion in space. The question asked by the detector is therefore not “what is the exact return” at time T, but something like “Is the return between -5% and +5%?
If the answer is “Yes”, the wave concentrates in the detector and collapses outside. If “No”, the wave collapses inside the detector. Then the wave starts again, affected by the measure, and expands until the next detection.
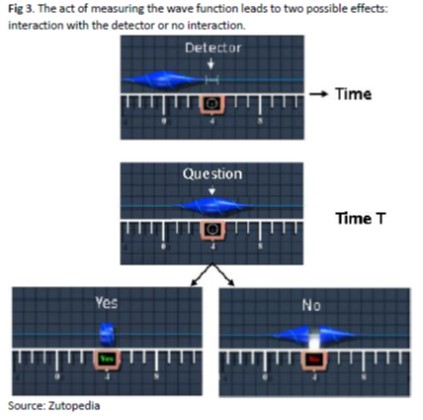
The detector’s positive or negative answer distorts the wave function in very different ways. The future will therefore look different depending on the past.
If the measurement is unsurprising (left representations), then the wave function is barely unchanged after expansion. If, however, the measure provides a surprising answer (right representations), then the wave function becomes skewed towards further surprises.

Let’s now run an experiment in finance, for instance the S&P since 1928. The monthly distribution, one month before the measure, is the unconditional distribution of returns split into six bars (lower returns than -2 standard deviations, between -2 and -1 std, between -1 and 0 std, between 0 and 1 std, between 1 and 2 std, and higher than 2std).
Assume that the S&P posts a “normal” return at a certain point in time. “Normal” means highly expected, for instance within -2std to +2std. The distribution of returns will barely be affected in the future, as represented in figure 5.
Now let us assume that the S&P posts a surprisingly high positive or negative monthly return, for instance outside the -2std to +2std range. One month later, we observe that the distribution of returns has been skewed towards the tails, like a quantum wave. This result is consistent with quantum physics.
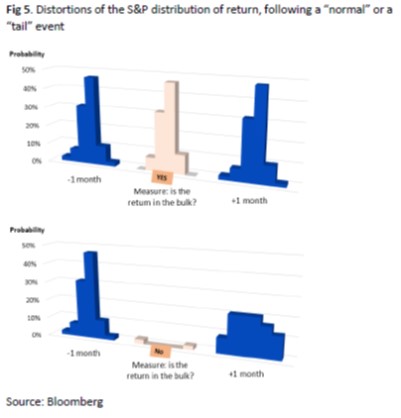
The conclusion is that the MSCI World behavior in the last few months is not surprising. Traditional financial interpretation is naive. Financial tail events do have consequences on future price movements. They increase the probability of further tail events. Furthermore, volatility spikes take time to amortize, like quantum waves of particles.
Memory sticks.
By Didier Darcet